Eigenvector와 Eigenvalue의 개념

참고 :

http://coolstu.blog.me/130176439747

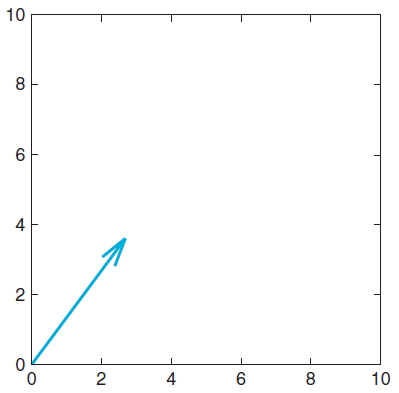
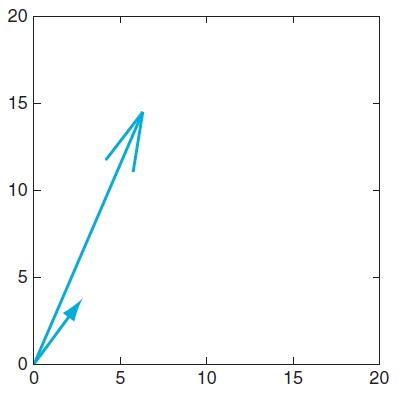
벡터 B가 (3 4)'라고 하면 좌표평면에서는 아래의 그림과 같이 표현될 수 있다. 

 

 

 

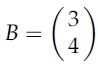
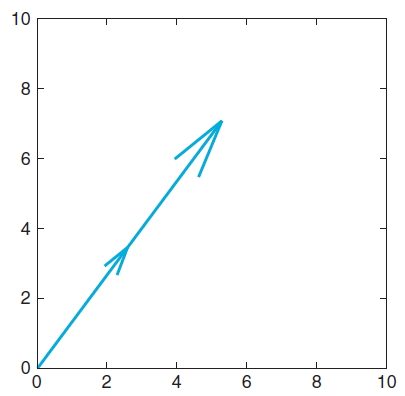
벡터 B에 상수 2를 곱하면 (6 8)'가 되는데, 이는 원래의 벡터에서 길이만 변하고 방향은 변하지 않는 것을 확인할 수 있다.

 

 

 

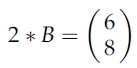
하지만 벡터 B에 행렬을 곱해주면 길이뿐만 아니라 방향도 변하는 것을 볼 수 있다.

 

 

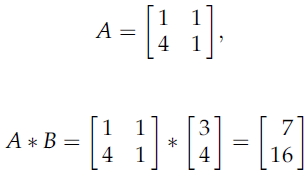
하지만 동일한 행렬 A에 벡터 (1, 2)'를 곱하면 방향은 변하지 않고 길이만 변하는 것을 확인할 수 있다.

 

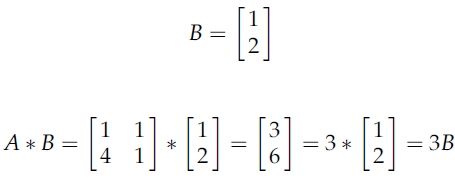
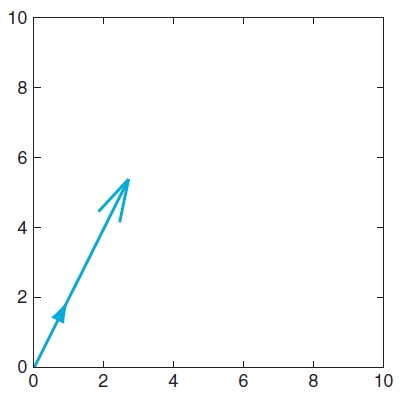
이것은 벡터 B에 행렬 A를 곱하는 것과 벡터 B에 상수 3을 곱하는 것이 같은 결과를 갖는 것을 보여준다.
따라서 아래와 같이 행렬 A에 대하여 다음 식을 만족하는 B와 람다가 존재한다

 

이때 람다를 행렬 A의 Eigenvalue (고유치)라고 하고 벡터 B는 고유치 람다에 해당하는 행렬 A의 Eigenvector (고유벡터)라고 한다.

 

이 처럼 행렬 A의 eigenvector와 eigenvalue를 찾는 문제를 생각해보자.

 

만약 벡터 B가 0 벡터라면 행렬 A가 무엇이든지 상관없이 위의 식은 성립한다.

 

 

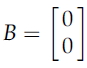
하지만 이것은 우리가 원하는 해답이 아니므로 0 벡터가 아닌 eigenvector를 구해보자.

 

람다에는 단위행렬이 곱해진 것과 같이 생각할 수 있으며, 우변의 식을 좌변으로 옮겨 B로 묶어주면 아래와 같이 표현될 수 있다.

 

이때 의 역행렬이 존재하여 양변에 역행렬을 곱해주면 아래와 같으며,

 

따라서 벡터 B는 0 벡터가 되게 된다.

 

따라서 의 역행렬이 존재하지 않아야 우리가 원하는 eigenvector와 eigenvalue를 구할 수 있으며,

 

그러기 위해서는 의 determinent가 0 이어야 한다.

 

 

이 식을 행렬 A의 Characteristic equation (특성방적식)이라고 한다.

 

행렬 A에 대하여 특성방정식을 풀어보면 아래와 같다.

 

 

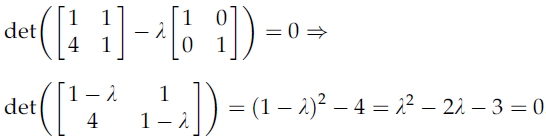
이를 만족하는 람다는 -1, 3이 있으며, 이는 행렬 A의 eigenvalue들이다.

 

각각의 람다를 식에 대입해보면 각 람다에 해당하는 eigenvector를 구할 수 있다.

 

먼저 식에 람다 3을 대입해보면, y=2x임을 알 수 있고 x에 임의의 수 1을 대입해보면 B=(1, 2)'의 eigenvector를 구할 수 있고,

 

 

람다 -1에 해당하는 eigenvector는 (1, -2)'인 것을 알 수 있다.

 

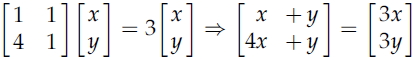
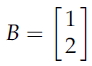
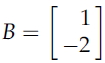
이때 행렬 A를 eigenvector와 eigenvalue로 표현할 수 있으며 이를 Eigendecomposition 이론이라고 한다.

 

행렬 V는 열이 eigenvector들인 정방행렬이며, D는 대각선의 각 요소가 eigenvalue인 정방대각선행렬이다.

 

위의 예로 설명을 하면 아래와 같다.

,

 

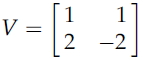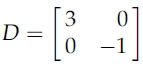
이때 V의 역행렬은 아래와 같고,

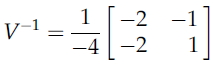
식을 계산해보면 행렬 A가 나오는 것을 확인할 수 있다.

 

 

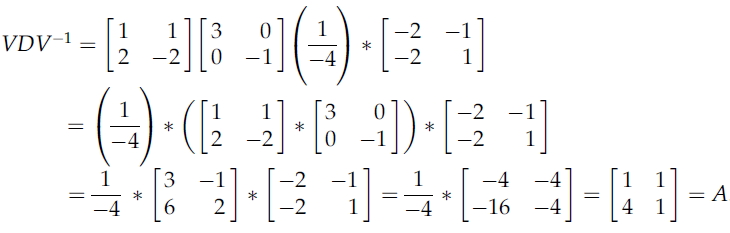
출처: Pascal Wallisch et al., Matlab for Neuroscientists, Academic Press, 2008